在学习Andrew Ng的机器学习课程Machine Learning,上了这个课之后感觉,这才叫MOOC好不好!老师很认真的在讲,而且讲的特别细致,连不会微积分都没关系( ̄▽ ̄)”
前两周的课程讲了线性回归的两种方法,一是梯度下降法(Gradient descent),二是正规方程(Normal Equation),两者各有利弊。
| 梯度下降法 | 正规方程 |
|---|---|
| 只能趋近于最优解 | 最优解√ |
| 需要选择合适的α | 有通式求解√ |
| O(n*iterations)√ | O(n^3) |
| 应用范围较广√ | 只能用于线性回归 |
根据Andrew老师的建议,当n(feature的种类)超过10000时,才应该考虑梯度下降法,否则用正规方程通常更好。
应用
用线性回归分析了一下学院上学期的成绩。
最可能会有相关关系的,是工数和线数。用正规方程求解,得到下图:
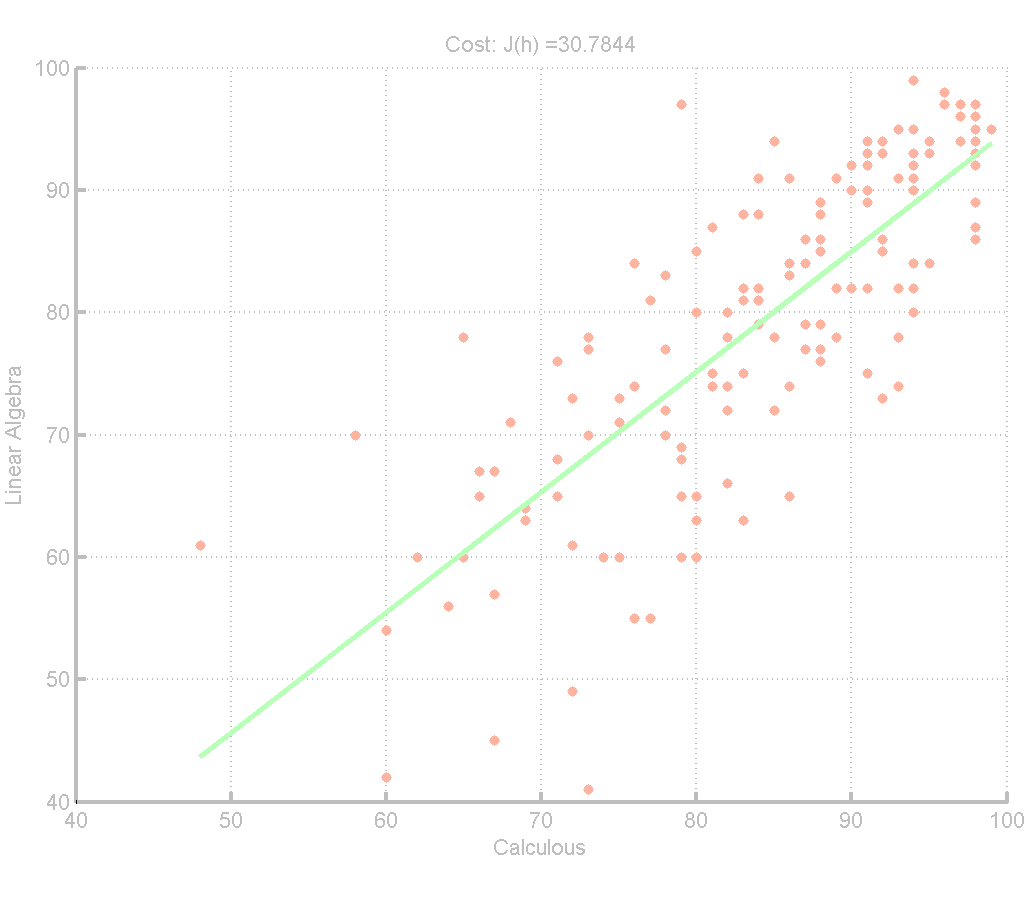
θ =
| -3.5127 |
| 0.9836 |
果然,θ2=0.98,说明这两门学科的分数是很有联系的。同时也看出了,工数的分数还是普遍高于线数的。有可能是因为工数的学分高,也有可能是确实线数比工数难一些吧。
之后用梯度下降法求解,得到了下图:
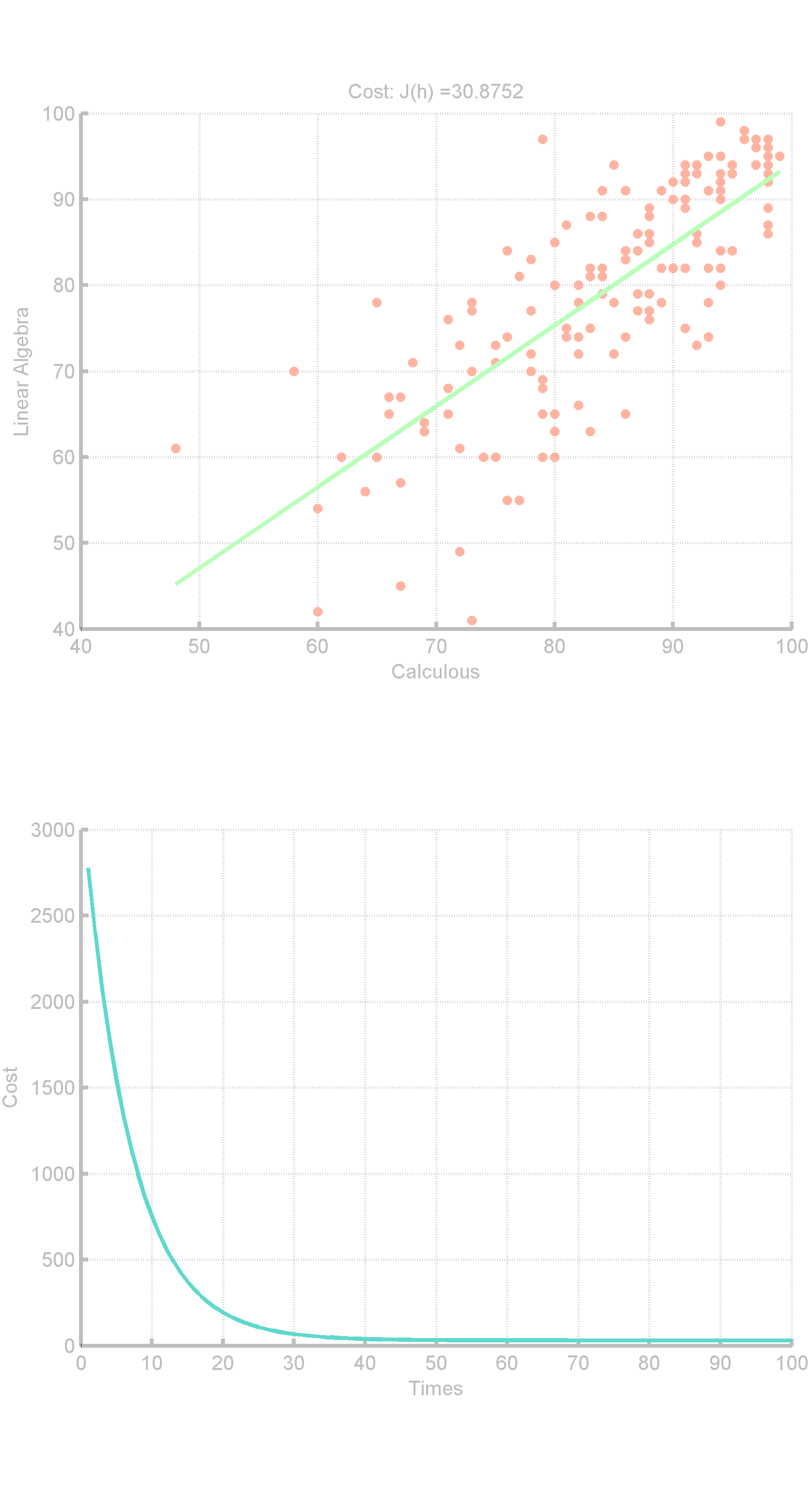
θ =
| 0.0110 |
| 0.9417 |
α =
0.00001
Andrew老师说将来会有方法自动选择α。但目前来看,这个α还是很难选的。而且这个梯度下降法,Cost的下降速度的下降速度(下降加速度)是很大的,只要α是能用的,差不多二三十次就能精确到个位了,但即使到了1000次(100次和1000次差别不大)还相差了0.8左右。可能真正使用梯度下降法的时候得迭代十万、百万次的。
其他
突然想看看,如果是没什么关系的数据,线性回归会得到什么结果呢?
于是,我计算了一下工数和军事理论的关系:
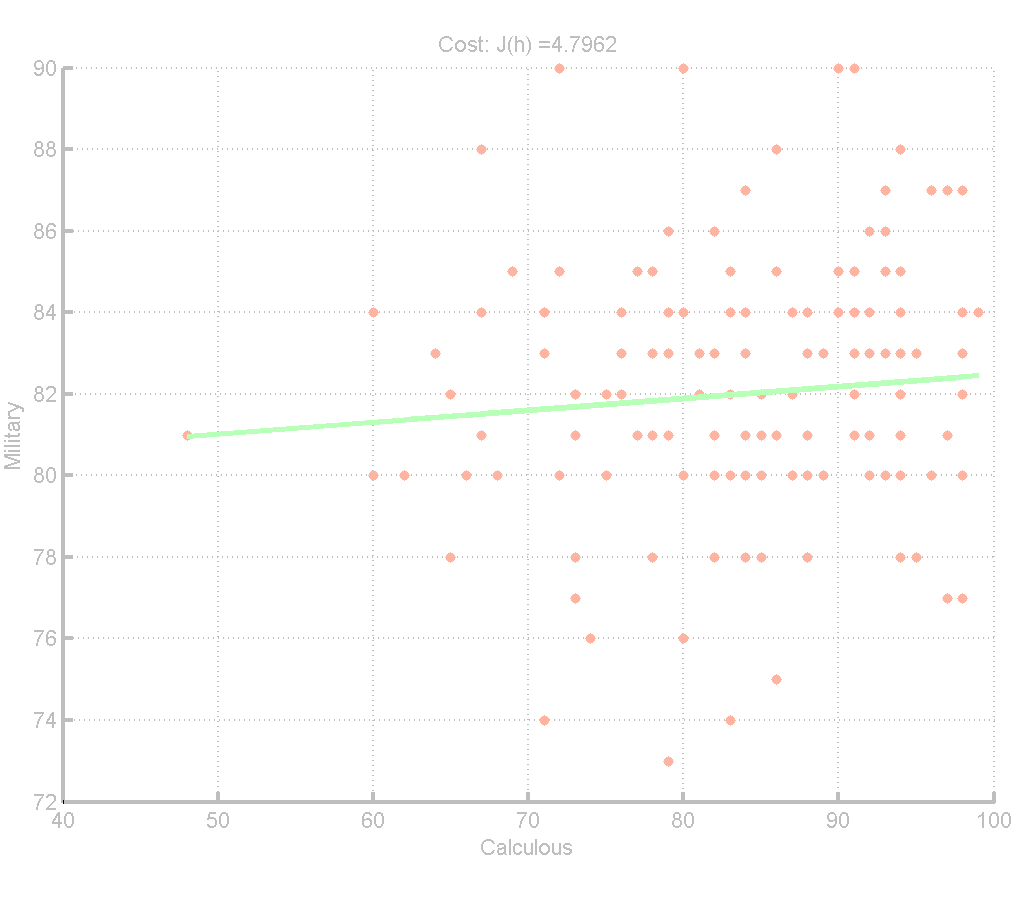
看到这个图的第一印象,这么分散啊,但看了一眼Cost,才4.8!看了一眼坐标轴,我想到了前两天知乎上看到的一个问题:「数据会说谎」的真实例子有哪些?今天碰见这张图,果然很有误导性啊,于是赶紧
set(gca, 'XLim', [40 100], 'YLim', [40 100]);
这样得到的图就合理多了:
.png)
这张图还让我明白,反应两个数据相关程度的并不是Cost的大小,而应该是对应的θ,θ越接近0,就越没关系。比如,当把工数和军理两科互换之后,Cost产生了很大的变化,但两者θ2都不大。
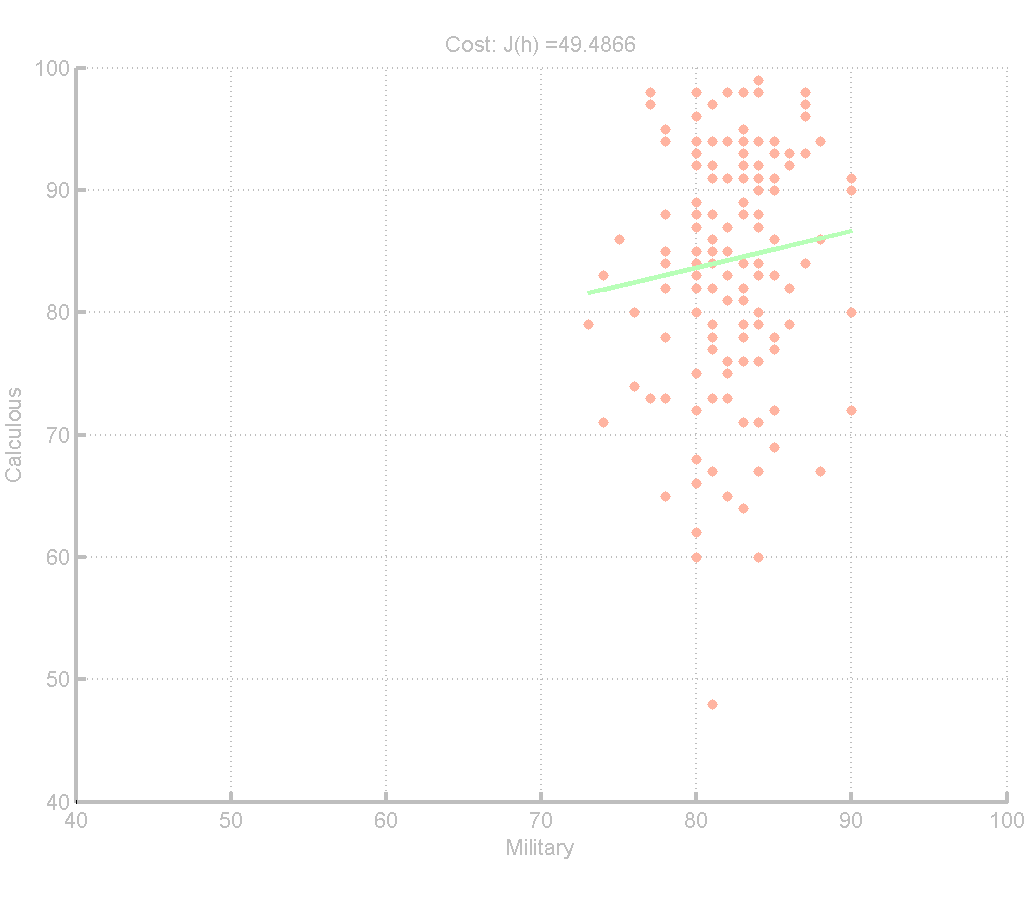
ps:其实我尝试过各种各样的组合,已经多个科目的组合,θ经常会降到0.1左右,甚至0.01左右,但从来没有小于0过。这说明,整体看来,“好学生”们,就算是那种凭运气的军理,也会比普通学生分数高一写,这应该就是态度不同的体现吧。