参加了老师的一个项目，要搞劣质数据对机器学习算法的影响，我负责实现DBSCAN算法。

定义

参数

ε(eps)：邻域半径

minPts：形成核心点最少的点数

距离

在二维（每个数据只有两个属性）的情况下，使用欧氏距离(sqrt(x^2+y^2))就可以有很好的效果，但对于更高维度的数据，欧氏距离是不适用的。

点的可达性

如果点p在距离ε内有至少minPts个点,则点p被称为核心点(core point)，p距离ε内的其他点被称为p的直接可达点(directly density-reachable point)。

对于点p和q，如果存在一个序列{p1,p2,…,pn}，其中p1=p，pn=1，满足∀i∈N,i<n有pi+1是pi的直接可达点，则称q为p的可达点(density-reachable point)。

对于点p和q，如果存在点o，p和q都是o的可达点，则称p和q是密度连接(density-connected)的。

如果点p不是任何点的可达点，则称p为局外点。

聚类

一个聚类满足如下性质：

聚类中的任意两个点都是密度连接的。

聚类中的任意点的可达点仍属于这个聚类。

算法

①对于每一个点，判断其是否为核心点

②新建一个聚类cluster

③找到一个没有被访问的点，放入cluster。如果所有店都被访问，则程序结束。

④根据cluster中点的可达点进行搜索，将搜索到的未被访问的点放入cluster，并标记为已访问。

⑤重复②

代码

#include <vector>
#include <algorithm>
#include <fstream>
#include <iostream>

#define pointSet std::vector<point>
#define pointerSet std::vector<int>

#define NOT_VISTED -1
#define WRITE_TO_FILE
#define ATTRIBUTIONS 4

#define minPts 4
#define E 0.1
//it is actually squared e

class point {
public:
	double a[ATTRIBUTIONS];
	int ddr;//amount of directly density-reachable points
	int flag;
	int flag_ans;
	pointerSet *ddrs;
	point(double *attributions, int flag_ans) {
		for (int i = 0; i < ATTRIBUTIONS; ++i) {
			a[i] = attributions[i];
		}
		ddr = 0;
		ddrs = NULL;
		flag = NOT_VISTED;
		this->flag_ans = flag_ans;
	}
	double distance(const point &p0) {
		double sum = 0;
		for (int i = 0; i < ATTRIBUTIONS; ++i) {
			sum += (a[i] - p0.a[i])*(a[i] - p0.a[i]);
		}
		return sum;//there is no sqrt() because E have been squared
	}
	bool operator < (const point &p0) {
		for (int i = 0; i < ATTRIBUTIONS; ++i) {
			if (a[i] < p0.a[i]) return true;
			else if (a[i] > p0.a[i]) return false;
		}
		return false;
	}
};

class DBSCAN {
public:
	DBSCAN(std::string file) {
		std::ifstream fin(file);
		fin >> N;
		for (int i = 0; i < N; ++i) {
			double attributions[ATTRIBUTIONS];
			int flag;
			for (int i = 0; i < ATTRIBUTIONS; ++i) {
				fin >> attributions[i];
			}
			fin >> flag;
			points.push_back(point(attributions, flag));
		}
		fin.close();
	}
	//To calcute ddr(amount directly density-reachable points) of every point and save ddrs(directly density-reachable points) for each CORE points
	void calcDdr(void) {
		for (int i = 0; i < N; i++) {
			pointerSet *p = new pointerSet;
			for (int j = 0; j < N; j++) {
				if (i == j) continue;
				if (points[i].distance(points[j]) < E) {
					points[i].ddr++;
					p->push_back(j);
				}
			}
			if (points[i].ddr >= minPts) {
				points[i].ddrs = p;
			}
			else {
				delete p;//if point i is not a core point, we need not to know its directly density-reachable points
			}
		}
	}
	void DFS(int x, int flag) {
		point &p = points[x];
		p.flag = flag;
		for (int i = 0; i < p.ddrs->size(); ++i) {
			if (points[p.ddrs->at(i)].flag == NOT_VISTED) {
				points[p.ddrs->at(i)].flag = flag;
				if (points[p.ddrs->at(i)].ddr >= minPts) DFS(p.ddrs->at(i), flag);
			}
		}
	}
	void process(void) {
		calcDdr();
		int flag = 0;
		for (int i = 0; i < N; ++i) {
			if (points[i].flag == NOT_VISTED && points[i].ddr >= minPts) {
				DFS(i, flag++);
			}
		}
#ifdef WRITE_TO_FILE
		std::ofstream fout("output.txt");
		for (int i = 0; i < N; ++i) {
			for (int j = 0; j < ATTRIBUTIONS; ++j) {
				fout << points[i].a[j] << '\t';
			}
			fout << points[i].flag << '\t' << points[i].flag_ans << std::endl;
		}
		fout.close();
#else
		for (int i = 0; i < N; ++i) {
			for (int j = 0; j < ATTRIBUTIONS; ++j) {
				std::cout << points[i].a[j] << ' ';
	}
			std::cout << points[i].flag << std::endl;
}
#endif
	}
private:
	int N;
	pointSet points;
};

int main()
{
	DBSCAN dbscan = DBSCAN("input.txt");
	dbscan.process();
	system("pause");
	return 0;
}

效果

二维的情况，看起来聚类的结果还是很好的，由于只使用了四个属性中的两个，所以没有将原始数据的三个集合给区分出来，但明显能看出来将相近的点分成了同样的颜色（灰色代表噪声）。

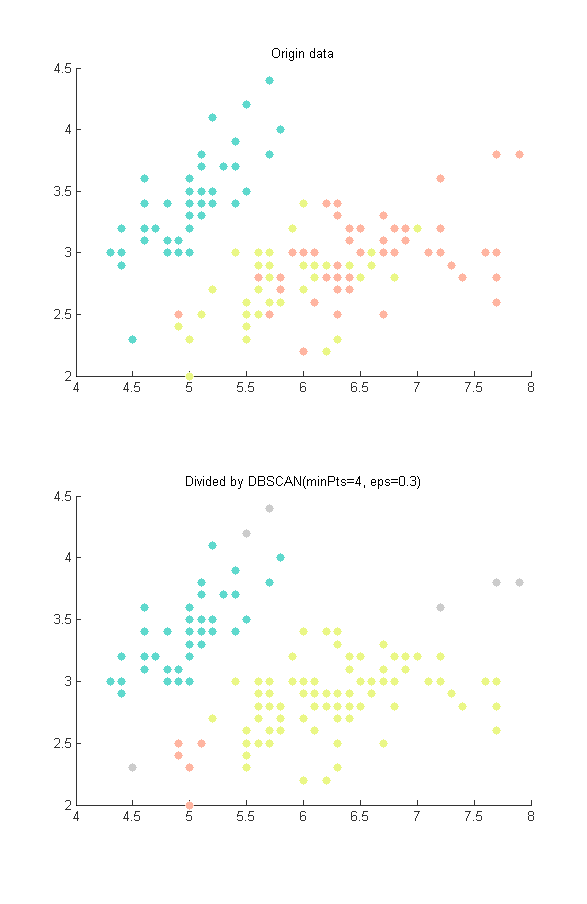
但在高维数据上，使用欧氏距离计算密度的DBSCAN的效果就不是很好了，甚至可以说非常不好，例如我用的iris数据，如果将四个属性全用上，则不管怎么调整参数，都无法大致将数据分成三类，虽然四维图像无法显示，但从输出来看，结果跟上图是差不多了，有两类无法分开。